Preprint: “On the Parameter Combinations That Matter and on Those That do Not”

Consider the function, depicted below, given by $f(x_1,x_2)=1+2e^{-3x_1x_2}-e^{x_1x_2}$, which is nominally defined in terms of two inputs. Both $x_1$ and $x_2$ influence the output, but only through the combination $\phi=x_1x_2$. Knowledge of the output is insufficient to identify a single pair of values for the corresponding inputs. Instead, we find an entire level set of inputs consistent with the observed output.

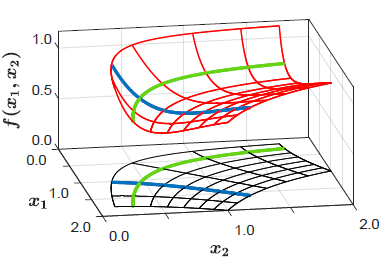
A function of two variables in which output behavior is determined solely by the effective parameter x_1x_2. Wire mesh (red) plotting function values and its projection (black) onto the domain. The green curve, on which f is constant, is a level set for the effective parameter. Conversely, f achieves all possible output values on the blue curve.

These level sets are one-dimensional curves in the two-dimensional domain, and there is a functional relationship between the two inputs when constrained to a particular output value. One could describe positions on such a level set using either $x_1$ or $x_2$. However, it is also possible to use the quantity $\psi=x_1^2−x_2^2$ to parameterize the level sets. This is convenient because $\phi$ and $\psi$ are conformal to each other. That is,

\[\nabla^\top\!\phi\;\nabla\psi=\begin{bmatrix}x_2 & x_1\end{bmatrix}\begin{bmatrix}2x_1 \\ -2x_2\end{bmatrix}=0\]

holds everywhere in the $(x_1,x_2)$ plane. Thus, $\phi$ and $\psi$ together form an orthogonal system of coordinates in which only one component influences the system output. We call the combination $\phi=x_1x_2$ an effective parameter, whereas $\psi=x_1^2-x_2^2$ is a redundant parameter.

This type of behavior, where the output from a system depends on relatively few effective parameters and other combinations of inputs are redundant, arises frequently in scientific applications. However, the effective parameters need not be physically meaningful, and a purely analytical strategy for model order reduction is not possible when the system behavior is available only as a black box. We propose a data-driven approach that can identify the number of effective parameter combinations on which the system’s behavior depends and provide a global parameterization in terms of a reduced set of coordinates.

Our framework offers various benefits. It identifies the intrinsic dimensinality of a system’s behavior without requiring any information beyond black-box observations. The number of effective parameters that we find implicitly tells us the number of redundant parameters as well, since the two must have a sum equal to the dimensionality of the input space. Our results are valid more than locally within a neighborhood of each experiment. We construct a parameterization that applies globally over the available data and allows for two-way prediction between observations and effective parameters.

Return to Research Page